Решения избранных задач из сборника "Задачи по элементарной физике". Законы сохранения импульса и механической энергии
27.2. Тело брошено вертикально вверх со скоростью \(V_{0}\) = 49 м/с. На какой высоте h его кинетическая энергия будет равна потенциальной? Ускорение свободного падения g = 9,8 \(м/с^{2}\). Потенциальную энергию в точке старта примите равной нулю.
Решение. Пренебрегая сопротивлением воздуха, запишем закон сохранения механической энергии:
$$\frac{mV_0^2}{2}=\frac{mV^{2}}{2}+mgh.\tag{10}$$
Здесь m - масса тела, h - искомая высота, V - скорость тела на высоте h. По условию задачи на этой высоте
$$\frac{mV^{2}}{2}=mgh.$$
Тогда из (10) имеем
$$\frac{mV_0^2}{2}=2mgh.$$
Откуда \(h=\frac{V_0^2}{4g}\approx61\) м. Найденная высота оказалась в два раза меньше максимальной высоты подъема камня над поверхностью земли \(h_{max}=\frac{V_0^2}{2g}.\)
27.5. С вершины гладкой наклонной плоскости высотой H = 20 см соскальзывает брусок. Определите скорость V бруска в конце плоскости. Ускорение свободного падения g = 10 \(м/с^{2}\). Начальная скорость равна нулю.
Решение. Примем основание горки за нулевой уровень потенциальной энергии. Поскольку трение отсутствует, механическая энергия бруска сохраняется. Приравнивая значения механической энергии на вершине горки и у ее основания, получим
$$0+mgh=\frac{mV^{2}}{2}+0.$$
Отсюда находим скорость бруска у основания плоскости:
$$V=\sqrt{2gh}= 20 м/с.$$
27.6. Шайба с нулевой начальной скоростью скользит с высоты H по гладкой наклонной плоскости, образующей угол α с горизонтом. В конце наклонной плоскости она встречает гладкую горизонтальную плоскость. Найдите максимальную высоту h подъема шайбы после абсолютно упругого удара о горизонтальную плоскость.
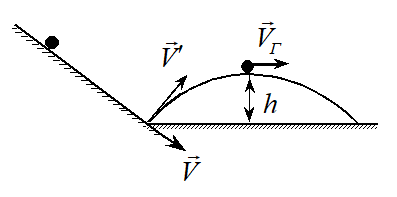
Решение. После отскока шайба будет двигаться по параболе (см. рис. 8). Для определения искомой высоты h проще всего воспользоваться законом сохранения механической энергии. На высоте h скорость шайбы имеет только горизонтальную составляющую \(\overrightarrow{V_{Г}}\). Приравнивая значения механической энергии в двух точках - на высоте H и в вершине параболы на высоте h - получим уравнение
$$0+mgh=\frac{mV_Г^2}{2}+mgh.$$
Величина скорости шайбы у основания наклонной плоскости равна \(V=\sqrt{2gh}\) (см. предыдущую задачу), а горизонтальная составляющая скорости \(V_Г=\sqrt{2gh}cosα\) при отскоке не изменяется. Следовательно, \(h=Hsin^{2}\alpha.\)