Физика для школьников и не только

Решения избранных задач из сборника "Задачи по элементарной физике". Кинематика. Часть 1

2.7. За третью секунду равноускоренного движения с начальной скоростью равной нулю тело проходит s₃ = 20 м. Найдите длину L пути за первые T = 5 с движения.

Решение. Из графика зависимости модуля скорости тела от времени видно, что пути, проходимые за 1-ую, 2-ую…5-ую секунды, относятся как 1:3:5:7:9.

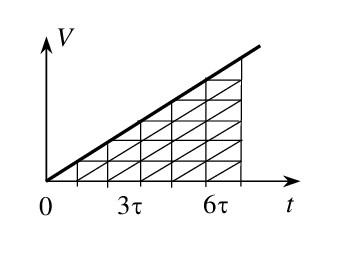
Следовательно,

$${s_3} = 5{s_1} = 5 \cdot \frac{{a{\tau ^2}}}{2}, \tag{1}$$

где s₁ – путь, пройденный за 1-ую секунду, a – ускорение тела, τ = 1 с. Путь, пройденный за время T,

$$L = \frac{{a{T^2}}}{2},$$

или, с учетом (1),

$$L = \frac{{{s_3}{T^2}}}{{5{\tau ^2}}} = 100 м.$$

5.1. Камень брошен вертикально вверх. На некоторой высоте камень оказывается через t₁ = 1 с и t₂ = 3 с после старта. Определите начальную скорость V₀ камня. Ускорение свободного падения g = 10 м/с².

Решение. В системе отсчета, связанной с Землей, движение камня является равноускоренным. Направим координатную ось y вертикально вверх, поместив ее начало на поверхность Земли. Тогда координата y тела меняется со временем по закону

$$y = {V_0}t - \frac{{g{t^2}}}{2}.$$

Запишем это равенство для моментов времени t₁ и t₂:

$${y_1} = {V_0}{t_1} - \frac{{gt_1^2}}{2},$$

$${y_2} = {V_0}{t_2} - \frac{{gt_2^2}}{2}.$$

Принимая во внимание, что \({y_1} = {y_2}\), получим $${V_0}{t_1} - \frac{{gt_1^2}}{2} = {V_0}{t_2} - \frac{{gt_2^2}}{2},$$

или

$${V_0} = \frac{{g({t_1} + {t_2})}}{2}= 20 м/с.$$

5.18. Тело свободно падает с нулевой начальной скоростью с высоты H = 45 м. Найдите среднюю скорость <V> падения на нижней половине пути. Ускорение свободного падения g = 10 м/с².

Решение. По определению средняя скорость \(< V > {\rm{ }} = l/t\), где l – путь, t – время, за которое этот путь пройден. Пусть t₁ - время, затраченное на первую половину пути, t₂ – полное время падения тела, тогда время движения тела на нижней половине пути \(t = {t_2} - {t_1}\). Времена t₁ и t₂ могут быть найдены из соотношений

$$H = \frac{{gt_2^2}}{2} \ и \ \frac{H}{2} = \frac{{gt_1^2}}{2}.$$
По условию задачи \(l = H/2\). Окончательно получаем

\( < V > = \frac{H}{{2({t_2} - {t_1})}} = \frac{{(\sqrt 2 + 1)}}{2}\sqrt {gH} \)= 25,6 м/с.

5.32. Тело брошено вертикально вверх с начальной скоростью V₀ = 3,13 м/с. Когда оно достигло наибольшей высоты подъема, из той же точки с такой же начальной скоростью брошено второе тело. На каком расстоянии s от точки старта встретятся тела? Ускорение свободного падения g = 9,8 м/с².

Решение. Направим координатную ось y вертикально вверх, поместив ее начало в точку бросания. Запишем зависимость координаты y каждого тела от времени, отсчитывая время от момента броска второго тела:

$${y_1} = {h_0} - \frac{{g{t^2}}}{2}, {y_2} = {V_0}t - \frac{{g{t^2}}}{2}.$$

Здесь \({h_0} = \frac{{V_0^2}}{{2g}}\) – высота, на которой находилось первое тело в момент броска второго. Условие встречи тел имеет вид $${y_1} = {y_2}.$$
Подставляя в последнюю формулу выражения для y₁ и y₂, находим время встречи тел:

$$t = \frac{{{h_0}}}{{{V_0}}} = \frac{{{V_0}}}{{2g}}.$$

Чтобы определить расстояние s от точки старта до места встречи тел, надо подставить это время в формулу для y₁ (или для y₂). В результате получаем

$$s = \frac{{3V_0^2}}{{8g}} \approx 0,375 м.$$

Замечание. Выражение для времени встречи \(t = \frac{{{h_0}}}{{{V_0}}}\) имеет такой вид, как если бы сближение тел происходило равномерно со скоростью V₀. Это не случайно: относительное движение двух тел, ускорения которых одинаковы, действительно является равномерным. Например, если оба тела (как в рассматриваемой задаче) совершают свободное движение в поле тяжести, то ускорение одного тела относительно другого равно \({\vec a_{12}} = {\vec a_1} - {\vec a_2} = \vec g - \vec g = 0\).