Физика для школьников и не только

Решения избранных задач из сборника "Задачи по элементарной физике". Кинематика. Часть 2

7.4. Эскалатор поднимает неподвижно стоящего на нем пассажира в течение t₁ = 1 мин. По неподвижному эскалатору пассажир поднимается за t₂ = 3 мин. Сколько времени t₃ будет подниматься идущий вверх пассажир по движущемуся вверх эскалатору?

Решение. Пусть l – длина эскалатора, V – его скорость, u – скорость пассажира относительно эскалатора. Тогда \(V = \frac{l}{{{t_1}}}\), \(u = \frac{l}{{{t_2}}}\) . Идущий вверх пассажир будет подниматься по движущемуся вверх эскалатору в течение времени \({t_3} = \frac{l}{{V + u}} = \frac{l}{{l/{t_1} + l/{t_2}}} = \frac{{{t_1}{t_2}}}{{{t_1} + {t_2}}} = \) 45 с.

7.6. Проплывая по реке под мостом против течения, лодочник потерял соломенную шляпу. Обнаружив пропажу через T = 10 мин, он повернул назад и подобрал шляпу на расстоянии l = 1 км ниже моста по течению. Определите скорость V течения реки. Считайте, что скорость лодки относительно воды постоянна.

Решение. Очевидно, скорость течения реки \(V = l/t\), где t – время, за которое шляпа проплыла путь l. Величину t проще всего найти, рассматривая движение в системе отсчета, связанной с водой. В этой системе вода неподвижна, а гребец плыл от шляпы и подплывал к ней с одной и той же скоростью и , следовательно, подобрал шляпу через время \(t = 2T\) после обнаружения пропажи. Окончательно имеем \(V = l/2T\) = 3 км/ч.

8.2. Тело брошено под углом \(\alpha\) = 30⁰ к горизонту с начальной скоростью V₀ = 10 м/с. Найдите величину V скорости тела через \(\tau\) = 1 с после начала движения и угол \(\beta\) между вектором \(\vec V\) и горизонтом. Ускорение свободного падения g = 10 м/с².

Решение. При описании движения тела, брошенного под углом к горизонту, удобно ось x прямоугольной системы координат направить горизонтально, ось y – вертикально вверх, начало координат поместить в точку бросания. Тогда при t = 0 компоненты скорости вдоль координатных осей могут быть записаны в виде

$${V_{0x}} = {V_0}\cos \alpha ,\ {V_{0y}} = {V_0}\sin \alpha .\tag{2}$$ При отсутствии сопротивления воздуха

$${a_x} = 0,\ {a_y} = - g. \tag{3}$$

Зависимость проекций скорости на оси координат от времени с учетом (2) и (3) принимает вид

$${V_x} = {V_0}\cos \alpha ,$$

$${V_y} = {V_0}\sin \alpha - gt.\tag{4}$$

Величина скорости тела в любой момент времени может быть найдена по формуле

$$V = \sqrt {V_x^2 + V_y^2} .$$

Подставляя в это выражение равенства (4), для величины скорости тела через время \(\tau\) после начала движения получим

$$V = \sqrt {V_0^2 - 2{V_0}\sin \alpha g\tau + {g^2}{\tau ^2}} = 10 м/с.$$

Угол между вектором скорости и горизонтом определяется соотношением

$$tg\beta = \frac{{{V_x}}}{{{V_y}}} = \frac{{{V_0}\sin \alpha - g\tau }}{{{V_0}\cos \alpha }} = tg\alpha - \frac{{g\tau }}{{{V_0}\cos \alpha }} = - \frac{1}{{\sqrt 3 }}.$$

В результате \(\beta\) = \( - \frac{\pi }{6}\).

8.11. Из одной точки одновременно бросают два тела - одно горизонтально, другое вертикально вверх с одинаковыми по величине скоростями V₀. На каком расстоянии s друг от друга окажутся тела через время t?

Решение. Задачу удобно решать в системе отсчета, связанной с одним из тел, поскольку в данном случае относительное движение тел является равномерным (см. замечание к задаче 5.32). В системе отсчета, связанной с первым телом, второе тело движется равномерно и прямолинейно со скоростью

$${\vec V_{21}} = {\vec V_{02}} - {\vec V_{01}},$$

где \({\vec V_{01}}\) и \({\vec V_{02}}\) – начальные скорости первого и второго тел соответственно. Следовательно, расстояние между телами зависит от времени по закону

$$s = \left| {{{\vec V}_{21}}} \right|t,$$

причем модуль относительной скорости в случае прямого угла между начальными скоростями определяется выражением

$$\left| {{{\vec V}_ { 21}}} \right|=\sqrt{V_{01}^2+V_{02}^2}=\sqrt{2}V_{0}.$$

Окончательно имеем \(s = \sqrt 2 {V_0}t\). Заметим, что величина относительной скорости зависит не от направления скоростей \({\vec V_{01}}\) и \({\vec V_{02}}\), а от угла между ними. Если, например, бросить тела с теми же по модулю скоростями, но под углами 30° и 120° к горизонту (в одной вертикальной плоскости), то ответ будет тот же.

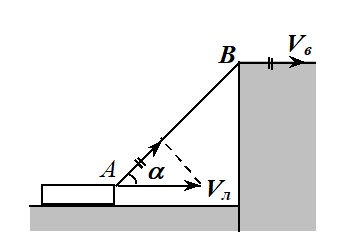
10.2. Стоящий на высоком берегу человек подтягивает лодку, выбирая с некоторой постоянной по величине скоростью V_в привязанную к носу лодки веревку. Определите величину V_л скорости лодки в момент, когда веревка составляет с горизонтом угол \(\alpha\).

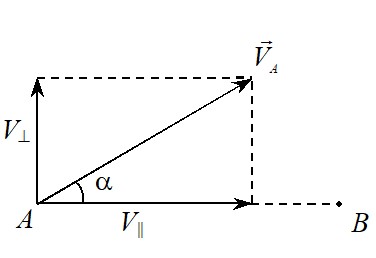
Решение. Для решения задачи воспользуемся достаточно очевидным кинематическим утверждением. Чтобы узнать, с какой скоростью движущаяся точка A приближается к неподвижной точке B (с какой скоростью уменьшается расстояние до этой точки, см. рис. 2), надо найти проекцию V_׀׀ скорости \({\vec V_A}\) на вектор \(\overrightarrow {AB}\) : \({V_{||}} = {V_A}\cos \alpha \). Понятно, что перпендикулярная составляющая скорости не изменяет расстояние между точками.

В данной задаче скорость, с которой точка A носа лодки приближается к точке B берега, где стоит человек (см. рис. 3), равна скорости вытягивания веревки V_в. Получаем для скорости лодки

$$V_{л} =\frac{V_{в}}{\cos\alpha }.$$