Физика для школьников и не только

Решения избранных задач из сборника "Задачи по элементарной физике". Кинематика. Часть 1

2.7. За третью секунду равноускоренного движения с начальной скоростью равной нулю тело проходит s₃ = 20 м. Найдите длину L пути за первые T = 5 с движения.

Решение. Из графика зависимости модуля скорости тела от времени видно, что пути, проходимые за 1-ую, 2-ую…5-ую секунды, относятся как 1:3:5:7:9.

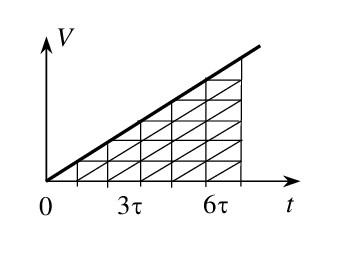
Следовательно,

$${s_3} = 5{s_1} = 5 \cdot \frac{{a{\tau ^2}}}{2}, \tag{1}$$

где s₁ – путь, пройденный за 1-ую секунду, a – ускорение тела, τ = 1 с. Путь, пройденный за время T,

$$L = \frac{{a{T^2}}}{2},$$

или, с учетом (1),

$$L = \frac{{{s_3}{T^2}}}{{5{\tau ^2}}} = 100 м.$$

5.1. Камень брошен вертикально вверх. На некоторой высоте камень оказывается через t₁ = 1 с и t₂ = 3 с после старта. Определите начальную скорость V₀ камня. Ускорение свободного падения g = 10 м/с².

Решение. В системе отсчета, связанной с Землей, движение камня является равноускоренным. Направим координатную ось y вертикально вверх, поместив ее начало на поверхность Земли. Тогда координата y тела меняется со временем по закону

$$y = {V_0}t - \frac{{g{t^2}}}{2}.$$

Запишем это равенство для моментов времени t₁ и t₂:

$${y_1} = {V_0}{t_1} - \frac{{gt_1^2}}{2},$$

$${y_2} = {V_0}{t_2} - \frac{{gt_2^2}}{2}.$$

Принимая во внимание, что \({y_1} = {y_2}\), получим $${V_0}{t_1} - \frac{{gt_1^2}}{2} = {V_0}{t_2} - \frac{{gt_2^2}}{2},$$

или

$${V_0} = \frac{{g({t_1} + {t_2})}}{2}= 20 м/с.$$

5.18. Тело свободно падает с нулевой начальной скоростью с высоты H = 45 м. Найдите среднюю скорость <V> падения на нижней половине пути. Ускорение свободного падения g = 10 м/с².

Решение. По определению средняя скорость \(< V > {\rm{ }} = l/t\), где l – путь, t – время, за которое этот путь пройден. Пусть t₁ - время, затраченное на первую половину пути, t₂ – полное время падения тела, тогда время движения тела на нижней половине пути \(t = {t_2} - {t_1}\). Времена t₁ и t₂ могут быть найдены из соотношений

$$H = \frac{{gt_2^2}}{2} \ и \ \frac{H}{2} = \frac{{gt_1^2}}{2}.$$
По условию задачи \(l = H/2\). Окончательно получаем

\( < V > = \frac{H}{{2({t_2} - {t_1})}} = \frac{{(\sqrt 2 + 1)}}{2}\sqrt {gH} \)= 25,6 м/с.

5.32. Тело брошено вертикально вверх с начальной скоростью V₀ = 3,13 м/с. Когда оно достигло наибольшей высоты подъема, из той же точки с такой же начальной скоростью брошено второе тело. На каком расстоянии s от точки старта встретятся тела? Ускорение свободного падения g = 9,8 м/с².

Решение. Направим координатную ось y вертикально вверх, поместив ее начало в точку бросания. Запишем зависимость координаты y каждого тела от времени, отсчитывая время от момента броска второго тела:

$${y_1} = {h_0} - \frac{{g{t^2}}}{2}, {y_2} = {V_0}t - \frac{{g{t^2}}}{2}.$$

Здесь \({h_0} = \frac{{V_0^2}}{{2g}}\) – высота, на которой находилось первое тело в момент броска второго. Условие встречи тел имеет вид $${y_1} = {y_2}.$$
Подставляя в последнюю формулу выражения для y₁ и y₂, находим время встречи тел:

$$t = \frac{{{h_0}}}{{{V_0}}} = \frac{{{V_0}}}{{2g}}.$$

Чтобы определить расстояние s от точки старта до места встречи тел, надо подставить это время в формулу для y₁ (или для y₂). В результате получаем

$$s = \frac{{3V_0^2}}{{8g}} \approx 0,375 м.$$

Замечание. Выражение для времени встречи \(t = \frac{{{h_0}}}{{{V_0}}}\) имеет такой вид, как если бы сближение тел происходило равномерно со скоростью V₀. Это не случайно: относительное движение двух тел, ускорения которых одинаковы, действительно является равномерным. Например, если оба тела (как в рассматриваемой задаче) совершают свободное движение в поле тяжести, то ускорение одного тела относительно другого равно \({\vec a_{12}} = {\vec a_1} - {\vec a_2} = \vec g - \vec g = 0\).

Решения избранных задач из сборника "Задачи по элементарной физике". Кинематика. Часть 2

7.4. Эскалатор поднимает неподвижно стоящего на нем пассажира в течение t₁ = 1 мин. По неподвижному эскалатору пассажир поднимается за t₂ = 3 мин. Сколько времени t₃ будет подниматься идущий вверх пассажир по движущемуся вверх эскалатору?

Решение. Пусть l – длина эскалатора, V – его скорость, u – скорость пассажира относительно эскалатора. Тогда \(V = \frac{l}{{{t_1}}}\), \(u = \frac{l}{{{t_2}}}\) . Идущий вверх пассажир будет подниматься по движущемуся вверх эскалатору в течение времени \({t_3} = \frac{l}{{V + u}} = \frac{l}{{l/{t_1} + l/{t_2}}} = \frac{{{t_1}{t_2}}}{{{t_1} + {t_2}}} = \) 45 с.

7.6. Проплывая по реке под мостом против течения, лодочник потерял соломенную шляпу. Обнаружив пропажу через T = 10 мин, он повернул назад и подобрал шляпу на расстоянии l = 1 км ниже моста по течению. Определите скорость V течения реки. Считайте, что скорость лодки относительно воды постоянна.

Решение. Очевидно, скорость течения реки \(V = l/t\), где t – время, за которое шляпа проплыла путь l. Величину t проще всего найти, рассматривая движение в системе отсчета, связанной с водой. В этой системе вода неподвижна, а гребец плыл от шляпы и подплывал к ней с одной и той же скоростью и , следовательно, подобрал шляпу через время \(t = 2T\) после обнаружения пропажи. Окончательно имеем \(V = l/2T\) = 3 км/ч.

8.2. Тело брошено под углом \(\alpha\) = 30⁰ к горизонту с начальной скоростью V₀ = 10 м/с. Найдите величину V скорости тела через \(\tau\) = 1 с после начала движения и угол \(\beta\) между вектором \(\vec V\) и горизонтом. Ускорение свободного падения g = 10 м/с².

Решение. При описании движения тела, брошенного под углом к горизонту, удобно ось x прямоугольной системы координат направить горизонтально, ось y – вертикально вверх, начало координат поместить в точку бросания. Тогда при t = 0 компоненты скорости вдоль координатных осей могут быть записаны в виде

$${V_{0x}} = {V_0}\cos \alpha ,\ {V_{0y}} = {V_0}\sin \alpha .\tag{2}$$ При отсутствии сопротивления воздуха

$${a_x} = 0,\ {a_y} = - g. \tag{3}$$

Зависимость проекций скорости на оси координат от времени с учетом (2) и (3) принимает вид

$${V_x} = {V_0}\cos \alpha ,$$

$${V_y} = {V_0}\sin \alpha - gt.\tag{4}$$

Величина скорости тела в любой момент времени может быть найдена по формуле

$$V = \sqrt {V_x^2 + V_y^2} .$$

Подставляя в это выражение равенства (4), для величины скорости тела через время \(\tau\) после начала движения получим

$$V = \sqrt {V_0^2 - 2{V_0}\sin \alpha g\tau + {g^2}{\tau ^2}} = 10 м/с.$$

Угол между вектором скорости и горизонтом определяется соотношением

$$tg\beta = \frac{{{V_x}}}{{{V_y}}} = \frac{{{V_0}\sin \alpha - g\tau }}{{{V_0}\cos \alpha }} = tg\alpha - \frac{{g\tau }}{{{V_0}\cos \alpha }} = - \frac{1}{{\sqrt 3 }}.$$

В результате \(\beta\) = \( - \frac{\pi }{6}\).

8.11. Из одной точки одновременно бросают два тела - одно горизонтально, другое вертикально вверх с одинаковыми по величине скоростями V₀. На каком расстоянии s друг от друга окажутся тела через время t?

Решение. Задачу удобно решать в системе отсчета, связанной с одним из тел, поскольку в данном случае относительное движение тел является равномерным (см. замечание к задаче 5.32). В системе отсчета, связанной с первым телом, второе тело движется равномерно и прямолинейно со скоростью

$${\vec V_{21}} = {\vec V_{02}} - {\vec V_{01}},$$

где \({\vec V_{01}}\) и \({\vec V_{02}}\) – начальные скорости первого и второго тел соответственно. Следовательно, расстояние между телами зависит от времени по закону

$$s = \left| {{{\vec V}_{21}}} \right|t,$$

причем модуль относительной скорости в случае прямого угла между начальными скоростями определяется выражением

$$\left| {{{\vec V}_ { 21}}} \right|=\sqrt{V_{01}^2+V_{02}^2}=\sqrt{2}V_{0}.$$

Окончательно имеем \(s = \sqrt 2 {V_0}t\). Заметим, что величина относительной скорости зависит не от направления скоростей \({\vec V_{01}}\) и \({\vec V_{02}}\), а от угла между ними. Если, например, бросить тела с теми же по модулю скоростями, но под углами 30° и 120° к горизонту (в одной вертикальной плоскости), то ответ будет тот же.

10.2. Стоящий на высоком берегу человек подтягивает лодку, выбирая с некоторой постоянной по величине скоростью V_в привязанную к носу лодки веревку. Определите величину V_л скорости лодки в момент, когда веревка составляет с горизонтом угол \(\alpha\).

Решение. Для решения задачи воспользуемся достаточно очевидным кинематическим утверждением. Чтобы узнать, с какой скоростью движущаяся точка A приближается к неподвижной точке B (с какой скоростью уменьшается расстояние до этой точки, см. рис. 2), надо найти проекцию V_׀׀ скорости \({\vec V_A}\) на вектор \(\overrightarrow {AB}\) : \({V_{||}} = {V_A}\cos \alpha \). Понятно, что перпендикулярная составляющая скорости не изменяет расстояние между точками.

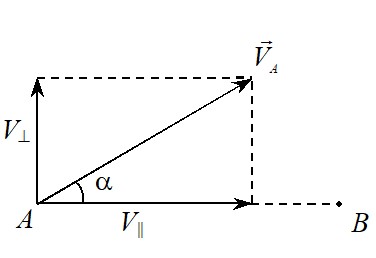
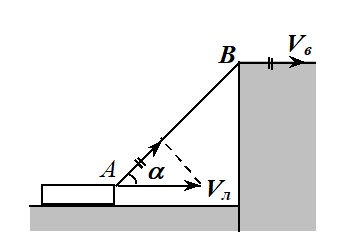
В данной задаче скорость, с которой точка A носа лодки приближается к точке B берега, где стоит человек (см. рис. 3), равна скорости вытягивания веревки V_в. Получаем для скорости лодки

$$V_{л} =\frac{V_{в}}{\cos\alpha }.$$

Решения избранных задач из сборника "Задачи по элементарной физике". Динамика

15.14. Брусок 1 массой \(m_{1}\) находится на гладкой горизонтальной плоскости. На бруске лежит тело 2 массой \(m_{2}\). Коэффициент трения между телом и бруском μ. При какой величине F силы, приложенной к бруску в горизонтальном направлении, тело начнет скользить по бруску? Ускорение свободного падения g .

Решение. Рассмотрим ситуацию «на грани проскальзывания»: тело и брусок еще движутся как одно целое, но сила трения покоя между ними уже достигла своего максимального значения

$$F_{тр} =μN. \tag{5}$$

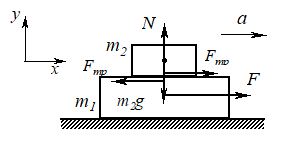
Удобно начать рассмотрение с тела, поскольку оно движется только под действием силы трения. Запишем второй закон Ньютона в проекции на оси выбранной системы координат (см. рис. 4):

$$m_{2}a=F_{тр},$$

$$0=N-mg. \tag{6}$$

Из (5) и (6) получаем \(F_{тр}=μm_{2}g,\) откуда a = µg. Именно при этом ускорении системы тело начнет скользить по бруску. Для определения силы F можно записать второй закон Ньютона для бруска (надо учесть, что на брусок со стороны тела действует сила трения, направленная «назад» и равная, в соответствии с третьим законом Ньютона, \(μm_{2}g\)). Но проще записать второй закон Ньютона для всей системы:

$$F=(m_{1}+m_{2})a=μ(m_{1}+m_{2})g.$$

15.15. К санкам массой \(m = (10⋅\sqrt{3}+1)\) кг, покоящимся на горизонтальной плоскости, приложили силу \(\overrightarrow{F},\) составляющую с горизонтом угол \(α = 30^{\circ}\). Вычислите минимальную величину этой силы, достаточную для начала движения санок. Коэффициент трения скольжения μ = 0,1. Ускорение свободного падения g = 10 \(м/с^{2}\).

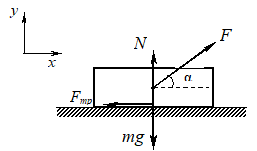
Решение. Величина приложенной к санкам силы будет минимальна, если движение санок равномерное. Учитывая это, запишем уравнение движения санок:

$$\overrightarrow{F}+m\overrightarrow{g}+\overrightarrow{F_{тр}}+\overrightarrow{N}=0.$$

Здесь \(\overrightarrow{F_{тр}}\) - сила трения, \(\overrightarrow{N}\) - нормальная составляющая реакции опоры. В соответствии с законом Амонтона-Кулона $$F_{тр} =μN. \tag{7}$$ Записывая проекции уравнения движения на оси координат, получим

$$Fcosα-F_{тр}=0,$$ $$Fsinα+N-mg=0.\tag{8}$$

Из (7) и (8) находим величину силы \(\overrightarrow{F}\):

$$F=\frac{μmg}{cosα+μsinα} = 20 Н.$$

15.37. Угол наклона плоскости доски к горизонту \(α = 30^{\circ}\). На доску положили кирпич массой m = 2 кг. Коэффициент трения скольжения кирпича по доске μ = 0,8. Найдите величину \(F_{тр}\) силы трения, действующей на кирпич. Ускорение свободного падения g = 10 \(м/с^{2}\).

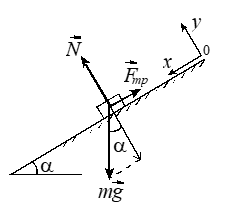
Решение. Исходя из соображений удобства, выберем систему координат так, как показано на рисунке. Изобразим все силы, действующие на кирпич. Прежде всего выясним, движется ли кирпич по наклонной плоскости. Если движется, то для нахождения силы трения скольжения можно воспользоваться законом Амонтона - Кулона (7)

$$F_{тр} =μN.$$

Если же кирпич не движется, то на него действует сила трения покоя.

Предположим, что кирпич движется вдоль наклонной плоскости с ускорением \(\overrightarrow{a}\). Запишем второй закон Ньютона в проекции на оси выбранной системы координат:

$$ma=mgsinα-F_{тр},$$ $$0=N-mgcosα. \tag{9}$$

Здесь учтено, что \(a_{x} = a,\) \(a_{y} = 0\). Из (9) определяем модуль нормальной составляющей реакции опоры:\(N=mgcosα\). Тогда \(F_{тр} = μmgcosα ≈\) 13,6 Н. С другой стороны, сила, которая вызывает движение кирпича по наклонной плоскости, - это со­ставляющая силы тяжести \(\overrightarrow{F}\) вдоль оси \(Ox\) (вдоль по­верхности соприкосновения тела и наклонной плоскости). Модуль этой составляющей равен \(F=mgsinα\) = 9,8 Н. Следовательно, \(F<F_{тр}.\) Это означает, что предположение о движе­нии кирпича было неверным. Кирпич покоится относительно наклонной плоскости, и на него действует сила трения покоя, равная по модулю составляющей силы тяжести вдоль оси \(Ox\), то есть \(F_{тр}=F=mgsinα\) = 9,8 Н. Направление силы трения покоя показано на рисунке. Найденная сила трения приложена к кирпичу. Заметим, что по третьему закону Ньютона такая же по модулю, но противоположная по направлению, сила трения покоя действует на наклонную плоскость, и приложена она к наклонной плос­кости.

20.16. Груз на нити описывает в горизонтальной плоскости окружность радиусом R = 10 см. Частота обращения груза n = 1 об/с. Какой угол α образует нить с вертикалью? Ускорение свободного падения g = 9,8 \(м/с^{2}\).

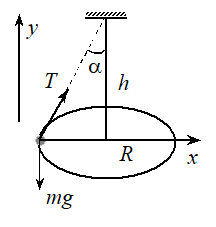
Решение. Уравнение движения груза в проекциях на горизонтальную (направленную к центру окружности) и вертикальную оси имеет вид

$$Tsinα=4π^{2}mn^{2}R,$$ $$Tcosα-mg=0,$$ где m - масса груза, T - сила натяжения нити. Исключая из этих уравнений силу натяжения нити, получаем $$tgα=\frac{4π^{2}n^{2}R}{g}.$$ В результате имеем $$α=arctg(\frac{4π^{2}n^{2}R}{g})\approx0,4.$$

Решения избранных задач из сборника "Задачи по элементарной физике". Законы сохранения импульса и механической энергии

27.2. Тело брошено вертикально вверх со скоростью \(V_{0}\) = 49 м/с. На какой высоте h его кинетическая энергия будет равна потенциальной? Ускорение свободного падения g = 9,8 \(м/с^{2}\). Потенциальную энергию в точке старта примите равной нулю.

Решение. Пренебрегая сопротивлением воздуха, запишем закон сохранения механической энергии:

$$\frac{mV_0^2}{2}=\frac{mV^{2}}{2}+mgh.\tag{10}$$

Здесь m - масса тела, h - искомая высота, V - скорость тела на высоте h. По условию задачи на этой высоте

$$\frac{mV^{2}}{2}=mgh.$$

Тогда из (10) имеем

$$\frac{mV_0^2}{2}=2mgh.$$

Откуда \(h=\frac{V_0^2}{4g}\approx61\) м. Найденная высота оказалась в два раза меньше максимальной высоты подъема камня над поверхностью земли \(h_{max}=\frac{V_0^2}{2g}.\)

27.5. С вершины гладкой наклонной плоскости высотой H = 20 см соскальзывает брусок. Определите скорость V бруска в конце плоскости. Ускорение свободного падения g = 10 \(м/с^{2}\). Начальная скорость равна нулю.

Решение. Примем основание горки за нулевой уровень потенциальной энергии. Поскольку трение отсутствует, механическая энергия бруска сохраняется. Приравнивая значения механической энергии на вершине горки и у ее основания, получим

$$0+mgh=\frac{mV^{2}}{2}+0.$$

Отсюда находим скорость бруска у основания плоскости:

$$V=\sqrt{2gh}= 20 м/с.$$

27.6. Шайба с нулевой начальной скоростью скользит с высоты H по гладкой наклонной плоскости, образующей угол α с горизонтом. В конце наклонной плоскости она встречает гладкую горизонтальную плоскость. Найдите максимальную высоту h подъема шайбы после абсолютно упругого удара о горизонтальную плоскость.

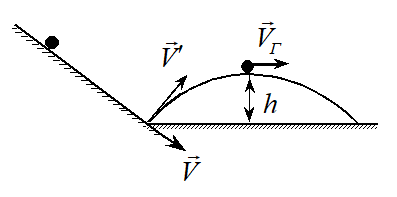
Решение. После отскока шайба будет двигаться по параболе (см. рис. 8). Для определения искомой высоты h проще всего воспользоваться законом сохранения механической энергии. На высоте h скорость шайбы имеет только горизонтальную составляющую \(\overrightarrow{V_{Г}}\). Приравнивая значения механической энергии в двух точках - на высоте H и в вершине параболы на высоте h - получим уравнение

$$0+mgh=\frac{mV_Г^2}{2}+mgh.$$

Величина скорости шайбы у основания наклонной плоскости равна \(V=\sqrt{2gh}\) (см. предыдущую задачу), а горизонтальная составляющая скорости \(V_Г=\sqrt{2gh}cosα\) при отскоке не изменяется. Следовательно, \(h=Hsin^{2}\alpha.\)