Демонстрационный вариант контрольной работы № 2

Тестовая часть

  1. Три маленьких шарика расположены в вершинах правильного треугольника. Момент инерции этой системы относительно оси \(O_{1}\), проходящей через два шарика, - \(I_{1}\). Момент инерции этой системы относительно оси \(O_{2}\), проходящей через середины двух соседних сторон треугольника, - \(I_{1}\).
    Среди приведенных ниже соотношений между моментами инерции системы относительно данных осей выберите верное.

Рис.1

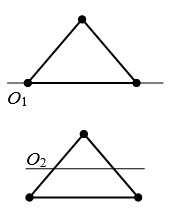
$$А)I_{1}>I_{2};\qquad Б) I_{1}=I_{2}; \qquadВ) I_{1}<I_{2}. $$

  1. Два диска с равными массами и радиусами \(R_{1}\) и \(R_{2}\) (\(R_{1}=2R_{2}\)) раскручивают из состояния покоя до одинаковых угловых скоростей. Найдите отношение совершенных работ \(A_{1}/A_{2}\). $$А)2;\qquad Б) 4; \qquad В) 1/2 \qquad Г) 1/4.$$

  2. Человек массой m стоит на краю горизонтального однородного диска массой M и радиусом R, который свободно вращается с угловой скоростью \(\omega_{0}\). Человек переместился на расстояние R/2 к центру диска и остановился (см. рис. 2). Пренебрегая размерами человека, найдите угловую скорость диска после перемещения человека.

Рис.2

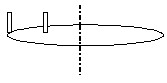
$$А)\omega=\omega_{0}\frac{M+2m}{M+m/2};\qquad Б) \omega=\omega_{0}\frac{M+2m}{M+m};\qquad В) \omega=\omega_{0}\frac{M+2m}{M}.$$

  1. Шар и сплошной цилиндр одинаковой массы и радиуса катятся без скольжения по горизонтальной поверхности с одинаковой скоростью. Кинетическая энергия шара меньше кинетической энергии цилиндра

    $$А)в 1,05 раза;\qquad Б) в 1,07 раза;$$
    $$В) в 1,10 раза;\qquad Г) в 1,25 раза.$$

  2. Импульс релятивистской частицы \(p=mc\). Определите отношение скорости частицы к скорости света в вакууме.

  3. Скорость релятивистской частицы массой m равна V = 0,6 c. Кинетическая энергия частицы

$$А)T=2mc^{2}/3;\qquad Б) T=mc^{2}/4;$$ $$В)T=mc^{2};\qquad Г) T=5mc^{2}/4;$$

  1. Материальная точка массой m = 10 г совершает колебания по закону \(x=0,02sin(\frac{\pi}{2}t+\frac{\pi}{4})\) (x, t - в единицах СИ). Максимальная сила, действующая на точку, равна

    $$А) 49 мН;\qquad Б) 20 мН;\qquad В) 0,31 мН;\qquad Г) 0,49 мН.$$

  2. Гармонический осциллятор совершает колебания. Какие из перечисленных ниже величин достигают максимального значения в момент прохождения грузом положения равновесия: скорость v, ускорение a, квазиупругая сила F, кинетическая энергия T, потенциальная энергия U?

    $$А) v, F, U ;\qquad Б) v, F, T;\qquad В) a, F, U; \qquad Г) v, T.$$

  3. Математический маятник совершает колебания по закону \(x=0,004cos(2t+0,8)\) (x, t - в единицах СИ). Длина нити маятника равна

    $$А) 4 м ;\qquad Б) 3,25 м ;\qquad В) 2,45 м ;\qquad Г) 0,25 м ;\qquad Д) 4 м.$$

  4. Какова амплитуда колебания, получающегося при сложении следующих гармонических колебаний одного направления: \(x_{1}=Asin2\piν\ \) , \(x_{2}=Asin(2\piν\ +2\pi/3)\)?

    $$А) A;\qquad Б)2A;\qquad В)A/2;\qquad Г)A/3.$$

  5. Расстояние между пучностью и ближайшим к ней узлом стоячей волны равно 20 см. Длина волны равна

    $$А)0,2 м;\qquad Б)0,4 м;\qquad В)0,8 м;\qquad Г) 0,3 м;\qquad Д) 0,1 м.$$

  6. В ходе некоторого равновесного процесса температура, объем и давление идеального газа связаны соотношениями \(T^{2}V=const, p \sim T^{n}.\) Масса газа постоянна. Найдите значение n.

$$А) -3;\qquad Б) -1;\qquad В) -2;\qquad Г) -1/2;\qquad Д) 3.$$

Задача

  1. Тонкий обруч, повешенный на вбитый горизонтально в стену гвоздь, совершает малые колебания в плоскости, параллельной стене. Радиус обруча R = 30 см. Определите период T колебаний обруча.

Ответы

  1. А
  2. Б
  3. А
  4. Б
  5. \(1/\sqrt{2}\)
  6. Б
  7. Г
  8. Г
  9. В
  10. А
  11. В
  12. Д
  13. 1,1 с