Демонстрационный вариант контрольной работы № 1

1-1

Закон Кулона. Напряженность электрического поля. Теорема Гаусса

1.

В точку A, расположенную вблизи неподвижного заряженного тела, поместили пробный заряд \(q_{1}\) и измерили действующую на него силу \(\overrightarrow{F_{1}}\) : \(F_{1x}\) = 3 мкН, \(F_{1y} =\) 4 мкН, \(F_{1z} = 0\). Затем заряд \(q_{1}\) убрали на большое расстояние, поместили в точку A другой пробный заряд \(q_{2}\) и измерили проекцию действующей на него силы: \(F_{2x} = \) - 9 мкН. Определите отношение \(q_{2}/q_{1}\).

2.

Точечные заряды \(-q\) и \(2q \) расположены в вершинах A и B прямоугольного равнобедренного треугольника АВС (С - вершина прямого угла). Во сколько раз уменьшится модуль вектора напряженности электрического поля в точке C, если заряд \(-q\) убрать?

3.

На рис. 1 изображен равномерно заряженный стержень AB длиной l и зарядом Q, а также воображаемая замкнутая поверхность в виде прямого цилиндра высотой h. Найдите поток вектора напряженности электрического поля через эту поверхность.

Рис.1

4.

При помощи теоремы Гаусса можно рассчитать напряженность электрического поля однородно заряженных
А) шара;
Б) бесконечно длинной нити;
В) кольца.

1-2

Потенциал. Проводники в электрическом поле. Диэлектрики

5.

Чтобы медленно переместить пробный заряд q = -100 нКл из точки 1 электростатического поля в точку 2 нужно совершить работу \(A_{12}\) = 100 нДж. Определите потенциал в точке 1, если потенциал в точке 2 равен нулю.

6.

В точках, лежащих на оси X, потенциал некоторого электростатического поля зависит от координаты x, как показано на рис. 2. В какой точке проекция вектора напряженности на ось X максимальна по модулю?

Рис.2

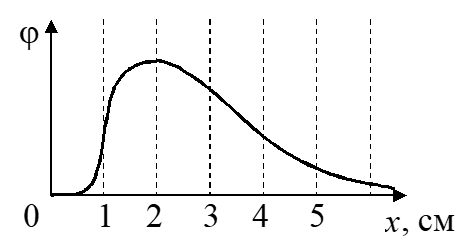
А) x = 1 см; Б) x = 2 см; В) x = 3 см; Г) x = 0.

7.

Какие из приведенных ниже формул для потенциала соответствуют одному и тому же электростатическому полю?

А) $$\phi=A\ln(B/\sqrt{x^{2}+y^{2}});$$ Б) $$\phi=2A\ln(B/\sqrt{x^{2}+y^{2}});$$ В) $$\phi=A\ln(2B/\sqrt{x^{2}+y^{2}}).$$

8.

Вблизи положительно заряженного металлического шара находится положительный точечный заряд q. Через какие замкнутые поверхности (одну или несколько) поток вектора напряженности электрического поля равен нулю?

Рис.3

9.

Как изменятся потоки векторов напряженности \(\overrightarrow{E}\) и индукции \(\overrightarrow{D}\) электрического поля через замкнутую поверхность S, которая охватывает часть наэлектризованного трением диэлектрика, если к диэлектрику поднести положительный точечный заряд?

Рис.4

А) поток вектора \(\overrightarrow{E}\) изменится, поток вектора \(\overrightarrow{D}\) не изменится;
Б) поток вектора \(\overrightarrow{D}\) изменится, поток вектора \(\overrightarrow{E}\) не изменится;
В) оба потока изменятся;
Г) оба потока не изменятся.

10.

1) Сформулируйте закон сохранения электрического заряда.
2) Запишите теорему Гаусса для вектора напряженности электрического поля.
3) Сформулируйте принцип суперпозиции электрических полей.
4) Запишите определение вектора поляризации.

1-3

Конденсаторы. Энергия электрического поля. Электрический ток

11.

Если радиус каждой обкладки сферического конденсатора увеличить в 2 раза, то емкость конденсатора

А) увеличится;
Б) уменьшится;
В) не изменится;
Г) может как увеличится, так и уменьшится в зависимости от радиуса внутренней обкладки.

12.

В вершинах равностороннего треугольника со стороной a расположены точечные заряды -q, +2q и +2q. Энергия взаимодействия этих зарядов равна

А) 0;
Б) \(\frac{{kq}^{2}}{a}\);
В) \(\frac{{4kq}^{2}}{a}\);
Г) \(\frac{{2kq}^{2}}{a}\).

13.

Ток в проводе увеличивается со временем t по закону \(I = {\alpha t}^{2}\), где \(\alpha\) - известная постоянная. За время от \(t_{1}\) = 0 до \(t_{2} = \tau\) через сечение провода пройдет заряд

А) \(q = {ατ}^{3}/3\);
Б) \(q = {ατ}^{2}S\), где S - площадь сечения;
В) \(q = {ατ}^{3}.\)

14.

Рис.5

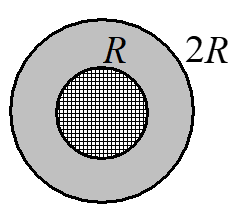
На рис. 5 показано поперечное сечение провода, изготовленного из двух различных проводников: внутреннего цилиндрического проводника радиуса R и внешнего проводника в виде цилиндрического слоя. Если при \(r < R\) модуль вектора плотности тока равен \(j_{1}\), а при \(R < r < 2R\) равен \(j_{2}\) (r - расстояние от оси симметрии провода), то величина тока через сечение провода равна

А) \(I=\pi R^{2}(j_{1}+j_{2});\)
Б) \(I=\pi R^{2}(j_{1}+2j_{2});\)
В) \(I=\pi R^{2}(j_{1}+3j_{2}).\)

15.

Определите работу электрических сил при уменьшении в 2 раза радиуса однородно заряженной сферы. Заряд сферы q, ее первоначальный радиус R.

Ответы

  1. -3
  2. \(\sqrt{5}\)/2
  3. \(Ф=Qh/\epsilon_{0}l\)
  4. А, Б
  5. 1 В
  6. А
  7. А, В
  8. В
  9. А
  10. см. конспект лекций
  11. А
  12. А
  13. А
  14. В
  15. \(A=- \frac{q^{2}}{8\pi \epsilon_{0}}\)