Демонстрационный вариант контрольной работы № 1
Тестовая часть
-
Материальная точка движется равномерно по окружности со скоростью \( v \) и за некоторое время проходит \( \frac{3}{4} \) окружности. Модуль вектора средней скорости точки за это время равен
А) \( \frac{3}{4\pi} v \);
Б) \( \frac{3\pi}{4} v \);
В) \( \frac{2\sqrt{2}}{3\pi} v \);
Г) \( \frac{2}{3\pi} v \).
-
Закон движения точки имеет вид \( \vec{r} = A t^2 \vec{i} + B t \vec{j} + C \vec{k} \), где \( A = 3 \ \text{м/с}^2 \), \( B = 4 \ \text{м/с}^2 \), \( C = 7 \ \text{м} \), \( \vec{i} \), \( \vec{j} \), \( \vec{k} \) — орты осей \( x \), \( y \) и \( z \) прямоугольной системы координат. Путь, пройденный точкой за первые \( t = 10 \ \text{с} \) движения, равен
А) 25 м;
Б) 100 м;
В) 150 м;
Г) 500 м;
Д) 707 м.
-
Твердое тело вращается вокруг неподвижной оси так, что угол поворота зависит от времени по закону \( \varphi = C t^3 \), где \( C = 1 \ \text{рад/с}^3 \). Угловая скорость тела в конце третьей секунды равна
А) 6 рад/с;
Б) 9 рад/с;
В) 27 рад/с.
-
Через блок, ось которого жестко закреплена, перекинута легкая нерастяжимая нить. К концам нити подвешены гири массами \( m_1 = m_2 = 1 \ \text{кг} \). Какую силу нужно приложить к одной из гирь, чтобы гири стали двигаться с ускорением \( a = 3 \ \text{м/с}^2 \)? Блок невесом, трение в оси блока отсутствует.
-
Небольшое тело массой \( m = 2 \ \text{кг} \) движется прямолинейно так, что пройденный путь зависит от времени по закону \( s = B t + C t^2 \), где \( B = 1 \ \text{м/с} \), \( C = 2 \ \text{м/с}^2 \). Сила, действующая на тело в конце первой секунды движения, равна
А) 2 Н;
Б) 4 Н;
В) 8 Н;
Г) 5 Н.
-
Вдоль оси \( Ox \) движутся две частицы, массы которых равны \( m_1 = 8 \ \text{г} \), \( m_2 = 1 \ \text{г} \), со скоростями \( V_{1x} = 1 \ \text{м/с} \) и \( V_{2x} = -28 \ \text{м/с} \) соответственно. В каком направлении движется центр масс системы?
А) в положительном направлении оси \( Ox \);
Б) в отрицательном направлении оси \( Ox \);
В) \( \vec{V}_c = 0 \).
-
Свободно падающий шарик массой \( m = 200 \ \text{г} \) ударился о пол, имея скорость \( v = 5 \ \text{м/с} \), и подпрыгнул на высоту \( h = 80 \ \text{см} \). Найдите модуль изменения импульса шарика при ударе. Сопротивлением воздуха пренебречь.
А) 0,2 кг·м/с;
Б) 0,8 кг·м/с;
В) 1,3 кг·м/с;
Г) 1,8 кг·м/с.
-
На частицу, находящуюся в начале координат, действует сила \( \vec{F} = 4 \vec{i} + 3 \vec{j} \), где \( \vec{i} \) и \( \vec{j} \) — орты осей \( x \) и \( y \) соответственно. Найдите работу, совершенную этой силой при перемещении частицы в точку с координатами \( (4, 3) \). Здесь компоненты силы и координаты частицы — в единицах СИ.
А) 9 Дж;
Б) 12 Дж;
В) 20 Дж;
Г) 25 Дж.
-
Работа консервативных сил
А) не зависит от формы пути и определяется только начальным и конечным положениями материальной точки;
Б) всегда равна нулю;
В) всегда положительна;
Г) всегда отрицательна.
-
Тело массой \( m = 1 \ \text{кг} \), брошенное с балкона в горизонтальном направлении со скоростью \( v_0 = 10 \ \ \text{м/с} \), через \( t = 1 \ \text{с} \) упало на землю. Определите кинетическую энергию \( T \), которую имело тело в момент удара о землю. Сопротивлением воздуха пренебречь.
-
Потенциальная энергия частицы, движущейся по оси \( Ox \) в силовом поле, \( U = -a x^2 \). При этом модуль ускорения точки \( a \sim x^n \). Найдите значение \( n \).
А) 1;
Б) 3;
В) 2;
Г) 1/2;
Д) 3/2.
-
Тело массы \( m \) бросили с башни высотой \( h \) со скоростью \( \vec{v}_0 \). Оно упало на землю со скоростью \( \vec{v} \). Работа силы сопротивления воздуха равна
А) \( A_{\text{сопр}} = mgh \);
Б) \( A_{\text{сопр}} = \frac{m}{2} (v^2 - v_0^2) - mgh \);
В) \( A_{\text{сопр}} = -\frac{m}{2} (v^2 - v_0^2) \);
Г) \( A_{\text{сопр}} = -\frac{m}{2} (v^2 - v_0^2) + mgh \).
Задача
- Точка движется, замедляясь, по окружности радиуса \( R \) так, что в каждый момент ее тангенциальное и нормальное ускорения одинаковы по модулю. В момент \( t = 0 \) скорость точки равна \( V_0 \). Найдите зависимость скорости \( V \) точки от времени.
Ответы
| Номер задания | Ответ |
|---|---|
| 1 | В |
| 2 | Г |
| 3 | В |
| 4 | 6 Н |
| 5 | В |
| 6 | Б |
| 7 | Г |
| 8 | Г |
| 9 | А |
| 10 | 100 Дж |
| 11 | А |
| 12 | Б |
| 13 | \( V = \frac{V_0}{1 + \frac{V_0}{R} t} \) |
Демонстрационный вариант контрольной работы № 2
Тестовая часть
- Три маленьких шарика расположены в вершинах правильного треугольника. Момент инерции этой системы относительно оси \(O_{1}\),
проходящей через два шарика, - \(I_{1}\). Момент инерции
этой системы относительно оси \(O_{2}\), проходящей через середины двух
соседних сторон треугольника, - \(I_{1}\).
Среди приведенных ниже соотношений между моментами инерции системы относительно данных осей выберите верное.
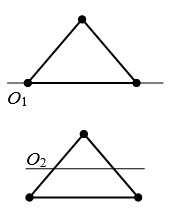
$$А)I_{1}>I_{2};\qquad Б) I_{1}=I_{2}; \qquadВ) I_{1}<I_{2}. $$
-
Два диска с равными массами и радиусами \(R_{1}\) и \(R_{2}\) (\(R_{1}=2R_{2}\)) раскручивают из состояния покоя до одинаковых угловых скоростей. Найдите отношение совершенных работ \(A_{1}/A_{2}\). $$А)2;\qquad Б) 4; \qquad В) 1/2 \qquad Г) 1/4.$$
-
Человек массой m стоит на краю горизонтального однородного диска массой M и радиусом R, который свободно вращается с угловой скоростью \(\omega_{0}\). Человек переместился на расстояние R/2 к центру диска и остановился (см. рис. 2). Пренебрегая размерами человека, найдите угловую скорость диска после перемещения человека.
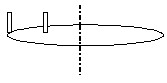
$$А)\omega=\omega_{0}\frac{M+2m}{M+m/2};\qquad Б) \omega=\omega_{0}\frac{M+2m}{M+m};\qquad В) \omega=\omega_{0}\frac{M+2m}{M}.$$
-
Шар и сплошной цилиндр одинаковой массы и радиуса катятся без скольжения по горизонтальной поверхности с одинаковой скоростью. Кинетическая энергия шара меньше кинетической энергии цилиндра
$$А)в 1,05 раза;\qquad Б) в 1,07 раза;$$
$$В) в 1,10 раза;\qquad Г) в 1,25 раза.$$ -
Импульс релятивистской частицы \(p=mc\). Определите отношение скорости частицы к скорости света в вакууме.
-
Скорость релятивистской частицы массой m равна V = 0,6 c. Кинетическая энергия частицы
$$А)T=2mc^{2}/3;\qquad Б) T=mc^{2}/4;$$ $$В)T=mc^{2};\qquad Г) T=5mc^{2}/4;$$
-
Материальная точка массой m = 10 г совершает колебания по закону \(x=0,02sin(\frac{\pi}{2}t+\frac{\pi}{4})\) (x, t - в единицах СИ). Максимальная сила, действующая на точку, равна
$$А) 49 мН;\qquad Б) 20 мН;\qquad В) 0,31 мН;\qquad Г) 0,49 мН.$$
-
Гармонический осциллятор совершает колебания. Какие из перечисленных ниже величин достигают максимального значения в момент прохождения грузом положения равновесия: скорость v, ускорение a, квазиупругая сила F, кинетическая энергия T, потенциальная энергия U?
$$А) v, F, U ;\qquad Б) v, F, T;\qquad В) a, F, U; \qquad Г) v, T.$$
-
Математический маятник совершает колебания по закону \(x=0,004cos(2t+0,8)\) (x, t - в единицах СИ). Длина нити маятника равна
$$А) 4 м ;\qquad Б) 3,25 м ;\qquad В) 2,45 м ;\qquad Г) 0,25 м ;\qquad Д) 4 м.$$
-
Какова амплитуда колебания, получающегося при сложении следующих гармонических колебаний одного направления: \(x_{1}=Asin2\piν\ \) , \(x_{2}=Asin(2\piν\ +2\pi/3)\)?
$$А) A;\qquad Б)2A;\qquad В)A/2;\qquad Г)A/3.$$
-
Расстояние между пучностью и ближайшим к ней узлом стоячей волны равно 20 см. Длина волны равна
$$А)0,2 м;\qquad Б)0,4 м;\qquad В)0,8 м;\qquad Г) 0,3 м;\qquad Д) 0,1 м.$$
-
В ходе некоторого равновесного процесса температура, объем и давление идеального газа связаны соотношениями \(T^{2}V=const, p \sim T^{n}.\) Масса газа постоянна. Найдите значение n.
$$А) -3;\qquad Б) -1;\qquad В) -2;\qquad Г) -1/2;\qquad Д) 3.$$
Задача
- Тонкий обруч, повешенный на вбитый горизонтально в стену гвоздь, совершает малые колебания в плоскости, параллельной стене. Радиус обруча R = 30 см. Определите период T колебаний обруча.
Ответы
- А
- Б
- А
- Б
- \(1/\sqrt{2}\)
- Б
- Г
- Г
- В
- А
- В
- Д
- 1,1 с
Вопросы к экзамену по дисциплине «Физика. Механика. Термодинамика»
(группы ИБ-11, МК-11, ПМ-11, ПМ-12, РТ-11, РТ-12, 1 семестр 2025/2026 уч. года)
-
Пространственно-временные системы отсчета:
- система отсчета;
- примеры систем координат, измерение длины;
- часы, измерение времени.
-
Способы описания движения материальной точки. Перемещение, скорость и ускорение:
- физические модели (материальная точка, система материальных точек, абсолютно твердое тело);
- способы описания движения (координатный, векторный, естественный);
- перемещение;
- вектор средней скорости, мгновенная скорость, среднее значение модуля скорости;
- среднее ускорение, ускорение.
-
Криволинейное движение материальной точки:
- тангенциальное ускорение;
- нормальное ускорение, радиус кривизны траектории.
-
Степени свободы и обобщенные координаты:
- степени свободы;
- обобщенные координаты;
- число степеней свободы абсолютно твердого тела.
-
Векторы элементарного углового перемещения, угловой скорости и углового ускорения:
- виды движения твердого тела (поступательное, вращательное, плоское);
- элементарное угловое перемещение, угловая скорость, угловое ускорение;
- связь между угловыми и линейными величинами при вращении твердого тела вокруг неподвижной оси.
-
Мгновенная ось вращения:
- мгновенное вращение, мгновенная ось;
- пример использования понятия мгновенной оси для описания движения твердого тела.
-
Инерциальные системы отсчета. Законы Ньютона:
- первый закон Ньютона;
- инерциальные системы отсчета;
- определение силы;
- масса, эталон массы, электронный килограмм;
- импульс;
- второй закон Ньютона;
- третий закон Ньютона.
-
Преобразования Галилея. Принцип относительности Галилея:
- преобразования Галилея;
- нерелятивистский закон сложения скоростей;
- инварианты преобразований Галилея;
- принцип относительности Галилея.
-
Силы в механике:
- гравитационная сила, сила тяжести;
- кулоновская сила;
- упругая сила;
- силы трения (сила трения покоя, сила трения скольжения, трение качения, вязкое трение);
- силы инерции.
-
Закон сохранения импульса:
- изолированная и замкнутая системы тел;
- закон сохранения импульса.
-
Теорема о движении центра масс. Система центра масс.
-
Работа и кинетическая энергия:
- работа силы, мощность;
- кинетическая энергия;
- теорема об изменении кинетической энергии;
- кинетическая энергия системы материальных точек.
-
Консервативные и неконсервативные силы. Потенциальная энергия:
- консервативные и неконсервативные силы;
- потенциальная энергия;
- потенциальная энергия тела в однородном поле тяжести;
- потенциальная энергия растянутой пружины;
- силы и потенциальная энергия.
-
Закон сохранения механической энергии:
- механическая энергия системы материальных точек;
- закон сохранения механической энергии.
-
Момент силы и момент импульса. Уравнение моментов:
- момент силы и момент импульса относительно точки;
- уравнение моментов;
- момент силы и момент импульса относительно оси.
-
Закон сохранения момента импульса:
- момент импульса системы материальных точек;
- закон сохранения момента импульса.
-
Уравнения движения и равновесия твердого тела:
- определение абсолютно твердого тела, твердое тело как система материальных точек;
- уравнения движения твердого тела;
- условия равновесия твердого тела.
-
Момент инерции тела относительно оси. Теорема Гюйгенса – Штейнера:
- момент инерции твердого тела относительно оси;
- примеры вычисления момента инерции в простейших случаях (однородный тонкий стержень, однородный сплошной цилиндр, однородный сплошной шар);
- теорема Гюйгенса – Штейнера.
-
Вращение твердого тела вокруг неподвижной оси:
- уравнение вращения твердого тела вокруг неподвижной оси;
- кинетическая энергия вращающегося твердого тела.
-
Работа внешних сил при вращении твердого тела вокруг неподвижной оси.
-
Плоское движение твердого тела:
- особенности описания плоского движения тела;
- кинетическая энергия тела при плоском движении.
-
Постулаты специальной теории относительности:
- дорелятивистские представления о пространстве и времени;
- опыты по обнаружению «мирового эфира», постоянство скорости света;
- постулаты специальной теории относительности.
-
Преобразования Лоренца:
- синхронизация часов, одновременность событий;
- преобразования Лоренца;
- обратные преобразования Лоренца.
-
Следствия преобразований Лоренца:
- относительность одновременности событий;
- сокращение длины движущегося тела;
- замедление хода движущихся часов;
- парадокс близнецов (парадокс часов).
-
Пространственно-временной интервал.
-
Релятивистские формулы сложения скоростей.
-
Релятивистский импульс.
-
Релятивистское уравнение движения.
-
Энергия релятивистской частицы:
- полная энергия релятивистской частицы;
- энергия покоя;
- кинетическая энергия релятивистской частицы.
-
Энергия, импульс и масса в специальной теории относительности:
- связь между энергией, импульсом и массой для свободно движущейся частицы;
- масса системы частиц (примеры).
-
Уравнение гармонических колебаний:
- кинематическая модель гармонических колебаний;
- амплитуда, частота и фаза гармонических колебаний;
- уравнение гармонических колебаний;
- общее решение уравнения гармонических колебаний.
-
Гармонические колебания груза на пружине.
-
Малые колебания математического и физического маятников.
-
Кинетическая и потенциальная энергия колеблющегося тела.
-
Метод векторных диаграмм. Сложение колебаний.
-
Биения.
-
Представление гармонических колебаний в комплексной форме.
-
Затухающие колебания:
- уравнение затухающих колебаний;
- решение уравнения затухающих колебаний;
- логарифмический декремент затухания;
- добротность колебательной системы.
-
Вынужденные колебания под действием синусоидальной силы:
- уравнение вынужденных колебаний;
- общее решение уравнения вынужденных колебаний при внешнем гармоническом воздействии;
- установившиеся вынужденные колебания.
-
Резонанс:
- зависимость амплитуды вынужденных колебаний от частоты;
- характеристики амплитудной резонансной кривой;
- резонанс;
- фазовая резонансная кривая.
-
Бегущие волны.
- определение волнового движения, продольные и поперечные волны;
- волновая поверхность, волновой фронт;
- плоские и сферические волны;
- уравнение плоской синусоидальной волны;
- фазовая скорость, длина волны.
-
Стоячие волны. Колебания струны.
-
Тепловое движение атомов и молекул. Температура:
- молекулярно-кинетическое и термодинамическое описание процессов;
- параметры состояния;
- температура, идеально-газовая шкала температур;
- температурные шкалы, используемые в быту и технике.
-
Идеальный газ. Уравнение состояния идеального газа.
-
Давление идеального газа.
-
Первое начало термодинамики:
- внутренняя энергия системы;
- первое начало термодинамики;
- первое начало термодинамики для элементарного процесса.
-
Обратимые и необратимые процессы:
- обратимые и необратимые процессы;
- равновесные процессы в идеальном газе (изотермический процесс, изобарный процесс, изохорный процесс, адиабатический процесс).
-
Тепловые машины. Цикл Карно:
- тепловые машины, коэффициент полезного действия тепловой машины;
- цикл Карно;
- коэффициент полезного действия цикла Карно.
-
Энтропия. Второе начало термодинамики. Теорема Нернста.
Лектор: Жаринова Н.Н.
Вектор напряженности
- На единицу длины тонкого однородно заряженного стержня АВ, имеющего форму дуги окружности радиуса R с центром в точке О, приходится заряд \(\lambda\). Найдите модуль напряженности электрического поля в точке О, если угол АОВ равен \(\phi\).
- Кольцо радиуса R из тонкой проволоки имеет однородно распределенный заряд q. Найдите модуль напряженности электрического поля на оси кольца как функцию расстояния y до его центра. Исследуйте \(E_{y}\) при \(y\gg R\).
- Находящийся в вакууме тонкий прямой стержень длины 2b заряжен однородно зарядом \(q>0\)._ Найдите модуль напряженности электрического поля как функцию расстояния r от центра стержня до точки прямой, совпадающей с осью стержня (r>b). Исследуйте полученное выражение при \(r\gg b\).
- Тонкий прямой стержень заряжен с линейной плотностью \(\lambda=\lambda_{0}(x/l)^{2}\), где l - длина стержня, x - расстояние от конца стержня, \(\lambda_{0}\) - положительная постоянная. Найдите модуль напряженности электрического поля при x = 0.
- Система состоит из тонкого заряженного проволочного кольца радиуса R и очень длинной однородно заряженной нити, расположенной по оси кольца так, что один из ее концов совпадает с центром кольца. Кольцо имеет заряд q>0. На единицу длины нити приходится заряд \(\lambda>0\). Найдите силу, с которой кольцо действует на нить.
Теорема Гаусса
-
Две однородно заряженные сферы имеют общий центр. Их радиусы равны R и 2 R, заряды соответственно 4 q и - q. Найдите модуль вектора напряженности электрического поля в точках, удаленных на расстояние r от центра сфер. Постройте график зависимости E(r).
-
Шар радиуса R имеет положительный заряд, объемная плотность которого зависит от расстояния r до его центра как \(\rho=\rho_0(1-r/R)\), где \(\rho_{0}\) - положительная постоянная. Пренебрегая влиянием вещества шара, найдите модуль вектора напряженности электрического поля внутри и вне шара как функцию r.
-
Электрическое поле создано двумя параллельными заряженными тонкими пластинами с поверхностными плотностями заряда \(+\sigma\) и \(-\sigma\). Площадь каждой пластины S, расстояние между пластинами d значительно меньше их продольных размеров. Определите:
а) напряженность электрического поля, созданного этими пластинами,
б) силу, с которой одна пластина действует на другую.
-
Поверхность бесконечного длинного кругового цилиндра заряжена однородно с линейной плотностью λ. Определите напряженность электрического поля внутри и вне цилиндра. Полученный результат представьте на графике \(E_{r}(r)\), где \(E_{r}\) - проекция вектора напряженности на ось r, перпендикулярную поверхности цилиндра, с началом отсчета на его оси симметрии.
Демонстрационный вариант контрольной работы № 1
1.
В точку A, расположенную вблизи неподвижного заряженного тела, поместили пробный заряд \(q_{1}\) и измерили действующую на него силу \(\overrightarrow{F_{1}}\) : \(F_{1x}\) = 3 мкН, \(F_{1y} =\) 4 мкН, \(F_{1z} = 0\). Затем заряд \(q_{1}\) убрали на большое расстояние, поместили в точку A другой пробный заряд \(q_{2}\) и измерили проекцию действующей на него силы: \(F_{2x} = \) - 9 мкН. Определите отношение \(q_{2}/q_{1}\).
2.
Точечные заряды \(-q\) и \(2q \) расположены в вершинах A и B прямоугольного равнобедренного треугольника АВС (С - вершина прямого угла). Во сколько раз уменьшится модуль вектора напряженности электрического поля в точке C, если заряд \(-q\) убрать?
3.
На рис. 1 изображен равномерно заряженный стержень AB длиной l и зарядом Q, а также воображаемая замкнутая поверхность в виде прямого цилиндра высотой h. Найдите поток вектора напряженности электрического поля через эту поверхность.

4.
При помощи теоремы Гаусса можно рассчитать напряженность электрического поля однородно заряженных
А) шара;
Б) бесконечно длинной нити;
В) кольца.
5.
Чтобы медленно переместить пробный заряд q = -100 нКл из точки 1 электростатического поля в точку 2 нужно совершить работу \(A_{12}\) = 100 нДж. Определите потенциал в точке 1, если потенциал в точке 2 равен нулю.
6.
В точках, лежащих на оси X, потенциал некоторого электростатического поля зависит от координаты x, как показано на рис. 2. В какой точке проекция вектора напряженности на ось X максимальна по модулю?
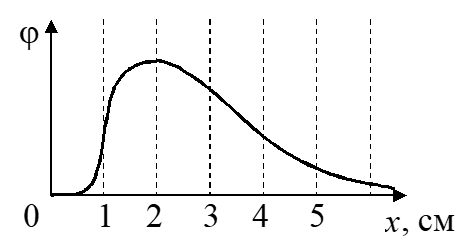
А) x = 1 см; Б) x = 2 см; В) x = 3 см; Г) x = 0.
7.
Какие из приведенных ниже формул для потенциала соответствуют одному и тому же электростатическому полю?
А) $$\phi=A\ln(B/\sqrt{x^{2}+y^{2}});$$ Б) $$\phi=2A\ln(B/\sqrt{x^{2}+y^{2}});$$ В) $$\phi=A\ln(2B/\sqrt{x^{2}+y^{2}}).$$
8.
Вблизи положительно заряженного металлического шара находится положительный точечный заряд q. Через какие замкнутые поверхности (одну или несколько) поток вектора напряженности электрического поля равен нулю?

9.
Как изменятся потоки векторов напряженности \(\overrightarrow{E}\) и индукции \(\overrightarrow{D}\) электрического поля через замкнутую поверхность S, которая охватывает часть наэлектризованного трением диэлектрика, если к диэлектрику поднести положительный точечный заряд?

А) поток вектора \(\overrightarrow{E}\) изменится, поток вектора \(\overrightarrow{D}\) не изменится;
Б) поток вектора \(\overrightarrow{D}\) изменится, поток вектора \(\overrightarrow{E}\) не изменится;
В) оба потока изменятся;
Г) оба потока не изменятся.
10.
1) Сформулируйте закон сохранения электрического заряда.
2) Запишите теорему Гаусса для вектора напряженности электрического поля.
3) Сформулируйте принцип суперпозиции электрических полей.
4) Запишите определение вектора поляризации.
11.
Если радиус каждой обкладки сферического конденсатора увеличить в 2 раза, то емкость конденсатора
А) увеличится;
Б) уменьшится;
В) не изменится;
Г) может как увеличится, так и уменьшится в зависимости от радиуса внутренней обкладки.
12.
В вершинах равностороннего треугольника со стороной a расположены точечные заряды -q, +2q и +2q. Энергия взаимодействия этих зарядов равна
А) 0;
Б) \(\frac{{kq}^{2}}{a}\);
В) \(\frac{{4kq}^{2}}{a}\);
Г) \(\frac{{2kq}^{2}}{a}\).
13.
Ток в проводе увеличивается со временем t по закону \(I = {\alpha t}^{2}\), где \(\alpha\) - известная постоянная. За время от \(t_{1}\) = 0 до \(t_{2} = \tau\) через сечение провода пройдет заряд
А) \(q = {ατ}^{3}/3\);
Б) \(q = {ατ}^{2}S\), где S - площадь сечения;
В) \(q = {ατ}^{3}.\)
14.
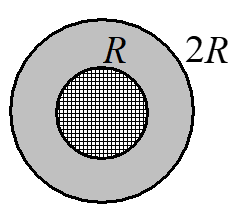
На рис. 5 показано поперечное сечение провода, изготовленного из двух различных проводников: внутреннего цилиндрического проводника радиуса R и внешнего проводника в виде цилиндрического слоя. Если при \(r < R\) модуль вектора плотности тока равен \(j_{1}\), а при \(R < r < 2R\) равен \(j_{2}\) (r - расстояние от оси симметрии провода), то величина тока через сечение провода равна
А) \(I=\pi R^{2}(j_{1}+j_{2});\)
Б) \(I=\pi R^{2}(j_{1}+2j_{2});\)
В) \(I=\pi R^{2}(j_{1}+3j_{2}).\)
15.
Определите работу электрических сил при уменьшении в 2 раза радиуса однородно заряженной сферы. Заряд сферы q, ее первоначальный радиус R.
- -3
- \(\sqrt{5}\)/2
- \(Ф=Qh/\epsilon_{0}l\)
- А, Б
- 1 В
- А
- А, В
- В
- А
- см. конспект лекций
- А
- А
- А
- В
- \(A=- \frac{q^{2}}{8\pi \epsilon_{0}}\)
1. Закон сохранения электрического заряда (формулировка).
2. Вектор напряженности электрического поля (определение).
3. Силовая линия электрического поля (определение).
4. Принцип суперпозиции электрических полей (формулировка).
5. Поток вектора напряженности электрического поля (определение).
6. Электростатическая теорема Гаусса в интегральной форме (формулировка, формула).
7. Разность потенциалов электрического поля (определение).
8. Потенциал электрического поля (определение).
9. Какие заряды называются связанными? сторонними?
10. Вектор поляризации (определение).
11. Аналог теоремы Гаусса для вектора поляризации в интегральной форме (формула).
12. Теорема Гаусса для вектора электрической индукции в интегральной форме (формулировка, формула).
Демонстрационный вариант контрольной работы № 2
1.
В формуле \( d \vec{B} = \frac{\mu_0 I}{4 \pi} \frac{[d \vec{l} \vec{r}]}{r^3} \), выражающей закон Био и Савара, вектор \( d \vec{l} \) означает
А) элемент провода с током, который создает поле \( d \vec{B} \);
Б) элемент провода с током, на который действует сила Ампера;
В) элемент произвольного замкнутого контура.
Ответ: А.
2.
Воображаемый замкнутый контур, образованный дугой окружности радиуса \( R \) и ее диаметром, расположен в вакууме в постоянном однородном магнитном поле, вектор \( \vec{B} \) индукции которого составляет угол \( \alpha \) с диаметром. Криволинейный интеграл \( \Gamma = \int \vec{B} d \vec{l} \) вдоль дуги окружности 1-2-3 равен
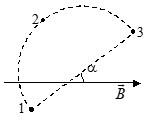
А) \( 2 \pi R B \cos \alpha \);
Б) \( 2 R B \cos \alpha \);
В) \( \pi R B \sin \alpha \);
Г) \( 2 R B \sin \alpha \).
Ответ: Б.
3.
Имеется длинный прямой провод круглого сечения радиуса \( R \), по которому течет ток \( I \), однородно распределенный по сечению. Воображаемый контур представляет собой окружность радиуса \( r < R \), плоскость которой перпендикулярна оси провода, а центр лежит на этой оси. Циркуляция вектора индукции магнитного поля по этому контуру равна
А) \( \mu_0 I (r / R)\);
Б) \( \mu_0 I (r / R)^2 \);
В) \( \mu_0 I (r / R)^3 \).
Ответ: Б.
4.
В однородном магнитном поле \( B \) находится контур с током, показанный на рисунке. Стороны 1, 2 и 3 имеют одинаковые длины. Запишите силы \( F_1, F_2, F_3, F_4, F_5 \), действующие со стороны магнитного поля на соответствующие стороны контура, в порядке возрастания их величин, начиная с наименьшей.
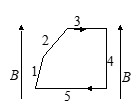
Ответ: \( F_4, F_1, F_2, F_3, F_5 \).
5.
На рисунке изображен круговой проводящий контур, помещенный в однородное магнитное поле, вектор индукции \( \vec{B} \) которого направлен от нас перпендикулярно плоскости чертежа. Индукционный ток в контуре протекает по часовой стрелке, если
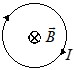
А) величина \( B \) растет;
Б) контур растягивается;
В) величина \( B \) убывает;
Г) контур сжимается.
Ответ: В, Г.
6.
В однородном магнитном поле с индукцией \( \vec{B} \) расположен П-образный проводник, плоскость которого перпендикулярна вектору магнитной индукции. По проводнику со скоростью \( V \) перемещают поступательно жесткую проводящую перемычку. В каких случаях ЭДС индукции в замкнутом контуре равна \( |\varepsilon| = BVl\)?
А) 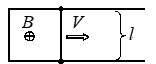 Б)
Б) 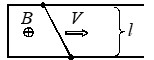 В)
В) 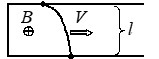
Ответ: А, Б, В.
7.
Укажите ошибочное утверждение:
А) изменение тока в контуре ведет к возникновению ЭДС индукции в этом же самом контуре, такое явление называется самоиндукцией;
Б) явление самоиндукции обусловлено действием магнитной составляющей силы Лоренца на носители тока в проводнике;
В) явление самоиндукции обусловлено действием вихревого электрического поля на носители тока в проводнике;
Г) самоиндукцию следует рассматривать как одно из проявлений электромагнитной индукции — ЭДС самоиндукции определяется формулой \( \varepsilon_s = -d \Phi / dt \).
Ответ: Б.
8.
Квадратная рамка со стороной \( a \), изготовленная из тонкой проволоки сопротивлением \( R \), находится в однородном магнитном поле, величина индукции которого зависит от времени по закону \( B = A t + D \), где \( A \) и \( D \) — постоянные. Вектор магнитной индукции составляет угол \( \alpha \) с нормалью к плоскости рамки. Определите зависимость индукционного тока в рамке от времени.
А) \( I(t) = \frac{2 a^2 A}{R} \sin \alpha \)
Б) \( I(t) = \frac{a^2 A}{R} \cos \alpha \)
В) \( I(t) = \frac{a^2 (A t + D)}{t R} \cos \alpha \)
Г) \( I(t) = \frac{a^2 (A t + D)}{t R} \sin \alpha \)
Ответ: Б.
9.
За миллисекунду амплитуда колебаний тока в колебательном контуре уменьшилась от \( I_0 = 5,4 \) мА до \( I_1 = 2 \) мА. Чему равен коэффициент затухания \( \beta \) колебаний?
Ответ: \( 1000 \ \text{с}^{-1} \).
10.
Магнитное поле порождают
А) постоянные токи;
Б) переменные токи;
В) движущиеся заряды;
Г) постоянное во времени неоднородное электрическое поле;
Д) переменное во времени электрическое поле.
Ответ: А, Б, В, Д.
11.
Укажите ошибочное утверждение, относящееся к плоской электромагнитной волне, распространяющейся в вакууме:
А) скорость волны равна \(c = 1 /\sqrt{\varepsilon_{0}\mu_{0}}\), где \(\varepsilon_0 \) и \( \mu_0 \) — электрическая и магнитная постоянные;
Б) в электромагнитной волне в любой момент времени векторы \( \vec{E}, \vec{B} \) и \( \vec{k} \) (волновой вектор) взаимно перпендикулярны;
В) в фиксированной точке пространства \( \vec{E} = \vec{E}_m \cos (\omega t + \alpha), \quad \vec{B} = \vec{B}_m \sin (\omega t + \alpha) \);
Г) \( \vec{E} = \vec{E}_m \cos (\omega t - \vec{k} \vec{r} + \alpha_0) \), где \( |\vec{k}| = 2 \pi / \lambda, \lambda \) — длина волны.
Ответ: В.
12.
Катушку подключили к источнику синусоидального напряжения постоянной амплитуды. С ростом частоты амплитуда тока через катушку
А) увеличивается;
Б) уменьшается;
В) не изменяется;
Г) может как увеличиваться, так и уменьшаться.
Ответ: Б.
13.
Угол между плоскостями пропускания двух идеальных поляризаторов \( \alpha_1 = 45^\circ \). Как изменится интенсивность прошедшего через них света, если этот угол уменьшить в 1,5 раза?
А) уменьшится в \( \sqrt{3} \) раза;
Б) уменьшится в 1,5 раза;
В) увеличится в 1,5 раза;
Г) увеличится в 2 раза.
Ответ: В.
14.
Свет падает на тонкую пленку с показателем преломления \( n \), большим, чем показатель преломления окружающей среды. Оптическая разность хода лучей на выходе из тонкой пленки равна
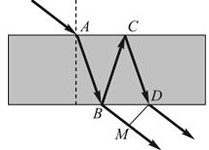
А) \( \Delta l = n (AB + BC) - \left( CD + \frac{\lambda}{2} \right) \);
Б) \( \Delta l = BC + CD + BM \);
В) \( \Delta l = BC + CD - BM \);
Г) \( \Delta l = n (BC + CD) - BM \).
Ответ: Г.
15.
Фазы колебаний, возбуждаемых в точке наблюдения двумя соседними зонами Френеля
А) совпадают;
Б) отличаются на \( \pi / 2 \);
В) отличаются на \( \pi \);
Г) отличаются на \( 2 \pi \) .
Ответ: В.
16.
Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (\(\lambda_1 = 0,50 \ \text{мкм} \)) заменить красным (\(\lambda_2 = 0,65 \ \text{мкм} \))?
Ответ: \( \frac{\lambda_2}{\lambda_1} = 1,3 \).