Демонстрационный вариант контрольной работы № 2

1.

В формуле \( d \vec{B} = \frac{\mu_0 I}{4 \pi} \frac{[d \vec{l} \vec{r}]}{r^3} \), выражающей закон Био и Савара, вектор \( d \vec{l} \) означает

А) элемент провода с током, который создает поле \( d \vec{B} \);
Б) элемент провода с током, на который действует сила Ампера;
В) элемент произвольного замкнутого контура.

Ответ: А.

2.

Воображаемый замкнутый контур, образованный дугой окружности радиуса \( R \) и ее диаметром, расположен в вакууме в постоянном однородном магнитном поле, вектор \( \vec{B} \) индукции которого составляет угол \( \alpha \) с диаметром. Криволинейный интеграл \( \Gamma = \int \vec{B} d \vec{l} \) вдоль дуги окружности 1-2-3 равен

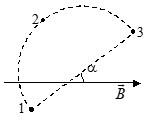
А) \( 2 \pi R B \cos \alpha \);
Б) \( 2 R B \cos \alpha \);
В) \( \pi R B \sin \alpha \);
Г) \( 2 R B \sin \alpha \).

Ответ: Б.

3.

Имеется длинный прямой провод круглого сечения радиуса \( R \), по которому течет ток \( I \), однородно распределенный по сечению. Воображаемый контур представляет собой окружность радиуса \( r < R \), плоскость которой перпендикулярна оси провода, а центр лежит на этой оси. Циркуляция вектора индукции магнитного поля по этому контуру равна

А) \( \mu_0 I (r / R)\);
Б) \( \mu_0 I (r / R)^2 \);
В) \( \mu_0 I (r / R)^3 \).

Ответ: Б.

4.

В однородном магнитном поле \( B \) находится контур с током, показанный на рисунке. Стороны 1, 2 и 3 имеют одинаковые длины. Запишите силы \( F_1, F_2, F_3, F_4, F_5 \), действующие со стороны магнитного поля на соответствующие стороны контура, в порядке возрастания их величин, начиная с наименьшей.

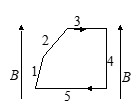
Ответ: \( F_4, F_1, F_2, F_3, F_5 \).

5.

На рисунке изображен круговой проводящий контур, помещенный в однородное магнитное поле, вектор индукции \( \vec{B} \) которого направлен от нас перпендикулярно плоскости чертежа. Индукционный ток в контуре протекает по часовой стрелке, если

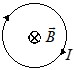
А) величина \( B \) растет;
Б) контур растягивается;
В) величина \( B \) убывает;
Г) контур сжимается.

Ответ: В, Г.

6.

В однородном магнитном поле с индукцией \( \vec{B} \) расположен П-образный проводник, плоскость которого перпендикулярна вектору магнитной индукции. По проводнику со скоростью \( V \) перемещают поступательно жесткую проводящую перемычку. В каких случаях ЭДС индукции в замкнутом контуре равна \( |\varepsilon| = BVl\)?

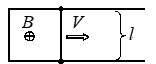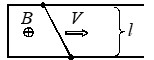А) Б) В)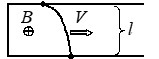

Ответ: А, Б, В.

7.

Укажите ошибочное утверждение:

А) изменение тока в контуре ведет к возникновению ЭДС индукции в этом же самом контуре, такое явление называется самоиндукцией;
Б) явление самоиндукции обусловлено действием магнитной составляющей силы Лоренца на носители тока в проводнике;
В) явление самоиндукции обусловлено действием вихревого электрического поля на носители тока в проводнике;
Г) самоиндукцию следует рассматривать как одно из проявлений электромагнитной индукции — ЭДС самоиндукции определяется формулой \( \varepsilon_s = -d \Phi / dt \).

Ответ: Б.

8.

Квадратная рамка со стороной \( a \), изготовленная из тонкой проволоки сопротивлением \( R \), находится в однородном магнитном поле, величина индукции которого зависит от времени по закону \( B = A t + D \), где \( A \) и \( D \) — постоянные. Вектор магнитной индукции составляет угол \( \alpha \) с нормалью к плоскости рамки. Определите зависимость индукционного тока в рамке от времени.

А) \( I(t) = \frac{2 a^2 A}{R} \sin \alpha \)
Б) \( I(t) = \frac{a^2 A}{R} \cos \alpha \)
В) \( I(t) = \frac{a^2 (A t + D)}{t R} \cos \alpha \)
Г) \( I(t) = \frac{a^2 (A t + D)}{t R} \sin \alpha \)

Ответ: Б.

9.

За миллисекунду амплитуда колебаний тока в колебательном контуре уменьшилась от \( I_0 = 5,4 \) мА до \( I_1 = 2 \) мА. Чему равен коэффициент затухания \( \beta \) колебаний?

Ответ: \( 1000 \ \text{с}^{-1} \).

10.

Магнитное поле порождают

А) постоянные токи;
Б) переменные токи;
В) движущиеся заряды;
Г) постоянное во времени неоднородное электрическое поле;
Д) переменное во времени электрическое поле.

Ответ: А, Б, В, Д.

11.

Укажите ошибочное утверждение, относящееся к плоской электромагнитной волне, распространяющейся в вакууме:

А) скорость волны равна \(c = 1 /\sqrt{\varepsilon_{0}\mu_{0}}\), где \(\varepsilon_0 \) и \( \mu_0 \) — электрическая и магнитная постоянные;
Б) в электромагнитной волне в любой момент времени векторы \( \vec{E}, \vec{B} \) и \( \vec{k} \) (волновой вектор) взаимно перпендикулярны;
В) в фиксированной точке пространства \( \vec{E} = \vec{E}_m \cos (\omega t + \alpha), \quad \vec{B} = \vec{B}_m \sin (\omega t + \alpha) \);
Г) \( \vec{E} = \vec{E}_m \cos (\omega t - \vec{k} \vec{r} + \alpha_0) \), где \( |\vec{k}| = 2 \pi / \lambda, \lambda \) — длина волны.

Ответ: В.

12.

Катушку подключили к источнику синусоидального напряжения постоянной амплитуды. С ростом частоты амплитуда тока через катушку

А) увеличивается;
Б) уменьшается;
В) не изменяется;
Г) может как увеличиваться, так и уменьшаться.

Ответ: Б.

13.

Угол между плоскостями пропускания двух идеальных поляризаторов \( \alpha_1 = 45^\circ \). Как изменится интенсивность прошедшего через них света, если этот угол уменьшить в 1,5 раза?

А) уменьшится в \( \sqrt{3} \) раза;
Б) уменьшится в 1,5 раза;
В) увеличится в 1,5 раза;
Г) увеличится в 2 раза.

Ответ: В.

14.

Свет падает на тонкую пленку с показателем преломления \( n \), большим, чем показатель преломления окружающей среды. Оптическая разность хода лучей на выходе из тонкой пленки равна

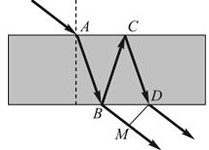
А) \( \Delta l = n (AB + BC) - \left( CD + \frac{\lambda}{2} \right) \);
Б) \( \Delta l = BC + CD + BM \);
В) \( \Delta l = BC + CD - BM \);
Г) \( \Delta l = n (BC + CD) - BM \).

Ответ: Г.

15.

Фазы колебаний, возбуждаемых в точке наблюдения двумя соседними зонами Френеля

А) совпадают;
Б) отличаются на \( \pi / 2 \);
В) отличаются на \( \pi \);
Г) отличаются на \( 2 \pi \) .

Ответ: В.

16.

Во сколько раз увеличится расстояние между соседними интерференционными полосами на экране в опыте Юнга, если зеленый светофильтр (\(\lambda_1 = 0,50 \ \text{мкм} \)) заменить красным (\(\lambda_2 = 0,65 \ \text{мкм} \))?

Ответ: \( \frac{\lambda_2}{\lambda_1} = 1,3 \).